Deadlock

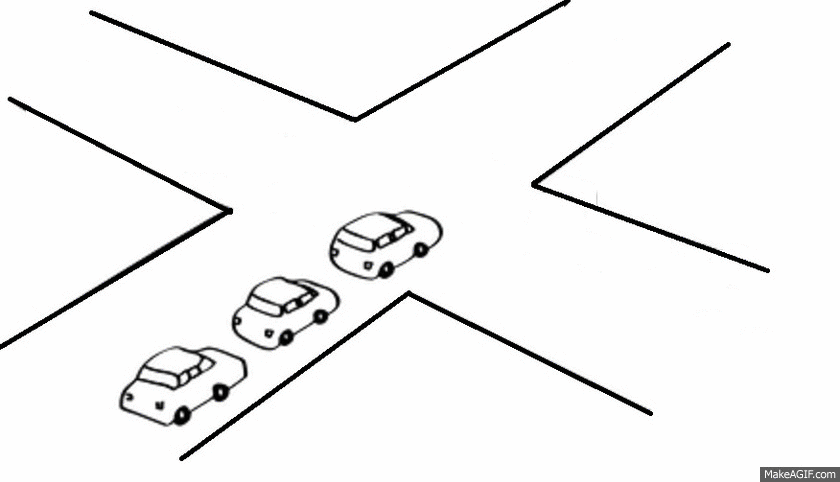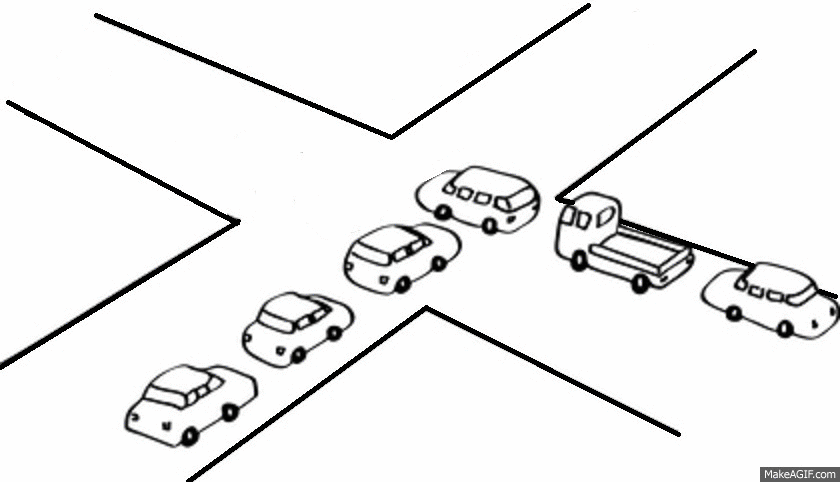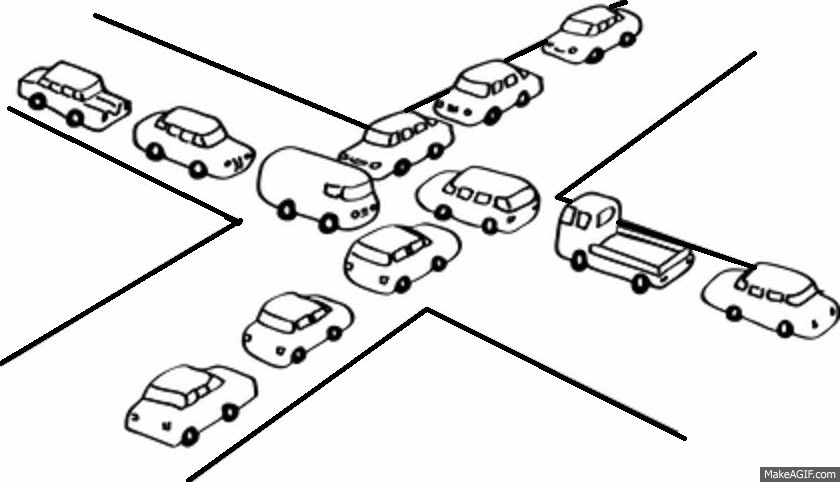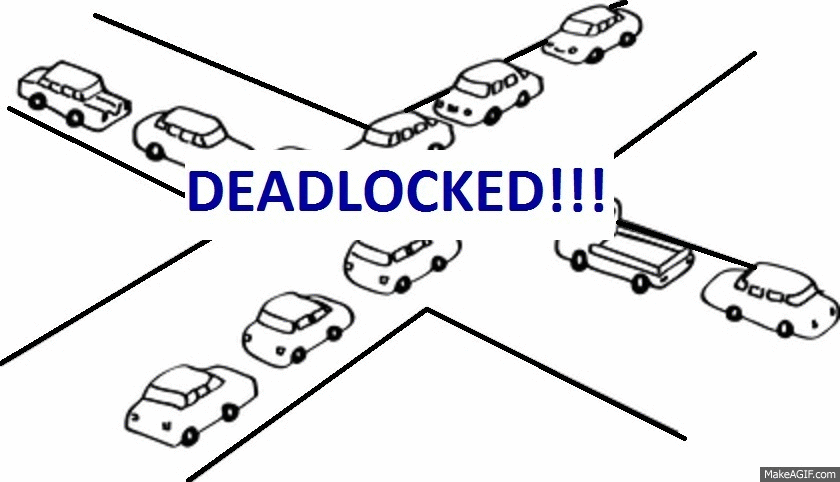
What is deadlock?

From wikipedia:

In an operating system, a deadlock occurs when a process or thread enters a waiting state because a requested system resource is held by another waiting process, which in turn is waiting for another resource held by another waiting process.

Coffman Conditions

Conditions on the system and its resources that are necessary and sufficient for deadlock to possibly occur.

So violating any condition = preventing deadlock!

1. Mutual Exclusion: No two processes can own a resource at the same time.
2. Circular Wait: There is a ‘cyclic dependency’ in processes owning and waiting for resources.
3. Hold and Wait: Once a process owns a resource, it retains that ownership, even while waiting for another.
4. Lack of Preemption: Processes cannot be forced to give up owned resources.

Dining philosophers

A good example of deadlock is the dining philosophers problem. In this problem, there are n philosophers trying to have dinner with n chopsticks. Each requires two chopsticks to eat. How can we allocate the chopsticks such that every philosopher gets to eat?

Who’s a good dining philosopher?

Solutions to the dining philsophers problem

Arbitrator

Have one authority (e.g. a mutex). Have each philosopher grab that authority and only when they have the authority can they pick up their forks and eat. They eat, put the arbitrator and the forks down and move on to the next philosopher (can be random or sequential).

Tradeoffs

• Very slow
• Only one thread running at a time
• Python’s global interpreter lock is implemented this way

Leave the table (Stallings)

Consider the case of the dining philosophers with n-chopsticks and n-philosophers. Reduce the number of philosophers currently allowed at the table to n-1 using a semaphore. Have them eat. Cycle out the philosophers.

Tradeoffs

• Very heavy on context switches for a process
• Needs way of “pausing” a philosopher (SIGSTOP for linux kernel)
• Need a “fair” cycling algorithm

Partial Ordering (Dijkstra)

Order the chopsticks 1..n. For each philosopher have them pick up the lower number chopstick. Then, only if they can pick up the lower chopstick, pick up the higher chopstick. Why does this work?

Tradeoffs

• Needs to be able to order the resources
• Doesn’t livelock but often leads one thread working at a time for large applications (databases)
• But good for dining philosophers!

BONUS: Clean/Dirty (Chandy/Misra)

(Beyond 341 scope) If you want a reeallly fast solution, given many philosophers numbered 1..n.

Relax problem assumptions– let philosophers talk to each other only to ask for chopsticks.

Chopsticks can be dirty or clean. Initially all start as dirty. For each pair of philosophers, assign the chopstick between them to the philosopher with the lower id. When one wants to eat, they ask their neighbor for a chopstick. If the neighbor’s chopstick is clean (they haven’t eaten yet), they keep the chopstick. Otherwise, they clean and relinquish it.

Tradeoffs

• Ensures priority is given to the philosopher that has least recently eaten (starvation prevention).
• Requires philosopher communication, so is not an exact instance of Dining Philosophers.
• Requires careful resource ordering to avoid an initial deadlock.

A good overview of solutions

Read the Ron Swanson version here

Resource allocation graph

We can model resource allocation by having resources and processes represented as vertices and use edges to show ownership of a resource. A cycle in the resource allocation graph implies that we can have deadlock (assuming other Coffman Conditions hold).

Example RAG

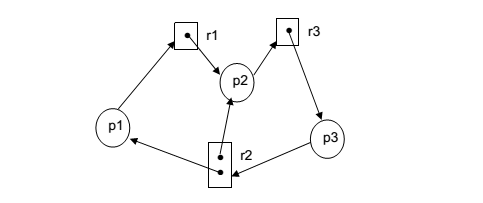
Relation to Dining Philosophers

The Dining Philosophers provide a more general view of preventing deadlock, and RAG analysis can be applied to some of our previous solutions. Replace ‘philosopher’ with ‘process’ and consider how our solutions stop a cycle.

• Arbitrator: The central authority is now the only dependency (forms a ‘star’ graph).
• Stallings: Remove a ‘process’, creating a path instead of a cycle.
• Ordering Solutions: Ensure that at least one ‘process’ always can get all resources through ordering (creates a sink node).

Questions?